Last week we talked about compression, where we went over the basics of compression and the two major categories (lossy and lossless). This week we will be going over a specific example of lossless compression Huffman Coding which is a text compression algorithm that is the predecessor for most current and more complex text compression methods. Before we get into how Huffman coding works, we need to go over some basics of how data is structured in a computer. As most of you know all data in a standard computer is stored in 1s and 0s or bits, every possible file is eventually boiled down to a chunk of 1s and 0s on a disk. We use different sized groups to represent different data types but a for a single English character in a text file we use 8 bits or 1 byte.
So, with that being said text file with each letter being 8 bits the amount of space can add up quickly, not really an issue for modern computers with terabytes of memory but for David Huffman in 1952 it was paramount to find a reliable and lossless compression solution, hence he developed what is now known as Huffman coding (2). Huffman coding takes advantage of statistical redundancies to compress a text file on average 30% which can make a huge difference, and the more statistical redundancies the higher the compression ratio goes up (1).
So, lets get into how Huffman coding works; say we took the title of this Dr. Seuss’ book
“One Fish Two Fish Red Fish Blue Fish”.
Right now, with spaces we have 36 characters in this quote which adds up to a total of 288 bits. Let us see if we can use Huffman code to get that down a little bit, first we need to count the occurrence of each letter (including spaces). Here are the occurrences of the letters in this sentence ordered most to least.
[space = 7, S = 4, F = 4, H = 4, I = 4, E = 3, O = 2, D = 1, W = 1, L = 1, N = 1, B = 1, R = 1, T = 1, U = 1]
As one might expect space is by far the most used character, now we must take this data and build it into a tree. Here is a quick video to show you how the tree is built.
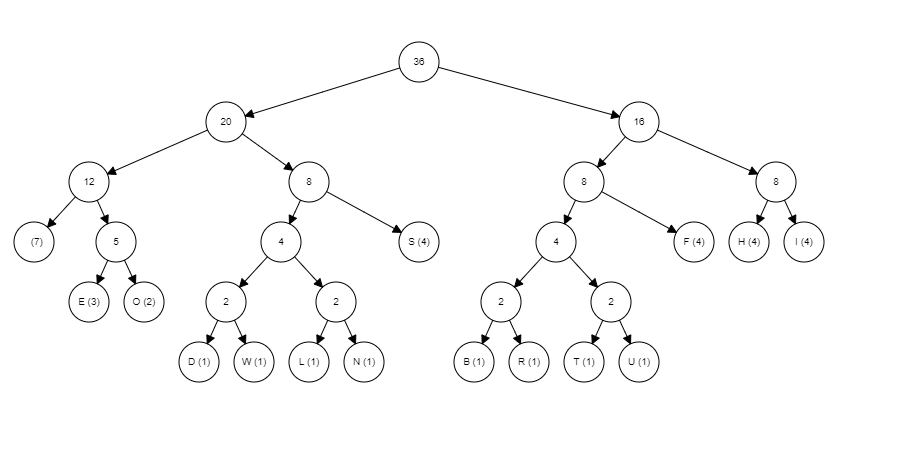
As you can see these graphs can get large pretty quick hence why I chose a sentence with a limited number of letters, now to interpret the graph. To interpret the graph, you need to know that any traversal to the left represents a zero and any traversal to the right represents a 1 and you always start from the root (node with the number 36 in it in this example). For example, the letter ‘S’s traversal from the root is left -> right -> right which is equal to 011 so now S can be represented as 011 five whole bits less than it was being presented by. Here is a list of the rest of the letters and their new bit representation.
[space = 000, S = 011, F = 101, H = 110, I = 111, E = 0010, O = 0011, D = 01000, W = 01001, L = 01010, N = 01011, B = 10000, R = 10001, T = 10010, U = 10011]
Now all letters are below 8 bits, therefore making the file compressed now adding up all the new bit amount times the frequencies of that letter the new total amount of bits used is 129 much less than the original 288, a whopping 55.2% reduction in size. Side note here Huffman Coding will not always make letter or symbols below 8 bits, when the tree gets large enough letters with very low frequency will go beyond 8 bits but this is still outweighed by the drastic reduction in bits used to represent the more used letters. Overall, compression is a very deep an interesting subject with a lot of detailed and interesting different methods for reducing file size; I encourage to look up other forms of compression for yourself.
Sources: