Radix Sort

               Today I would like to talk about my personal favorite sorting algorithm, radix sort. I realize that even saying I have a favorite sorting algorithm I just outed myself as a complete utter nerd although in my view that ship sailed a long time ago. In short radix is a sorting algorithm that uses the digits of each individual element in an array to put the elements into corresponding ‘buckets’ and then orders the array in the corresponding order of the buckets. The algorithm then proceeds to go over the new array again and again until the elements are all sorted. Here is a gif to make that a little less confusing.

Radix sort is actually one of the oldest sorting algorithms developed. It was developed all the way back in 1887 by Herman Hollerith which means that radix sort was developed before even the invention of the ballpoint pen let alone a modern computer (Herman). The algorithm was originally created for use in the tabulating machine that developed for the 1890 US Census to summarize punch card information (Columbia). Radix sort did not come back into use again until the 1920’s when it was found to be an efficient way to sort punch cards and was used by companies like IBM.

Radix sort was eventually computerized in 1954 by the MIT professor Harold H. Seward bringing it into the modern era. Now radix can be used for a variety of collections but most commonly integer or binary string collections. Compared to some of the ‘newer’ sorts, radix sort may seem to lack some complexity but that is its charm. In my opinion radix sort shows the ingenuity of Herman Hollerith invention at a time when there were not organized concepts of programming languages or programmable computers.

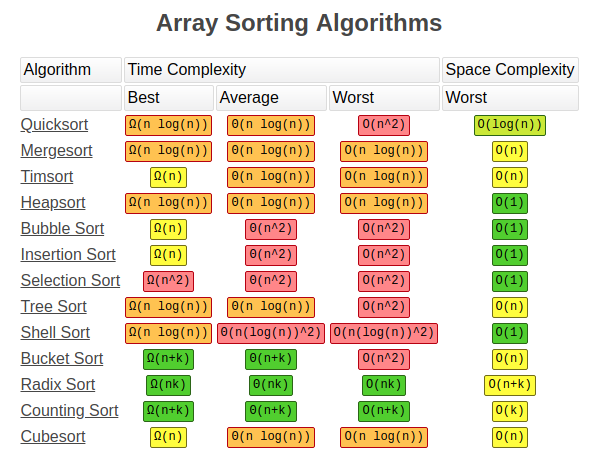
Radix sort is neither the quickest nor the slowest sorting algorithm, coming somewhere in the middle in terms of time required to complete a sort. Where radix earns respect is it is one of the most consistent, where worst and best case are both O(nk). Along with this, it is a non-comparative algorithm meaning that no two objects in the collection are ever compared to each other. For me personally I love radix sort as it was the first sorting algorithm that I learned about where it seemed to be a genuinely unique solution. Its uniqueness made me think differently about sorting and computer science in general. Whenever I program and have to sort something, make a visited hash, or any kind of key value pair I think back to radix sort as it was the first aha moment of my programming career, and it reminds me how truly great coding is when you can have such limitless solutions for a single problem.

RUBY CODE:

  def radix_sort(base=10)
    ary = dup
    rounds = (Math.log(ary.minmax.map(&:abs).max)/Math.log(base)).floor + 1
    rounds.times do |i|
      buckets = Array.new(2*base){[]}
      base_i = base**i
      ary.each do |n|
        digit = (n/base_i) % base
        digit += base if 0<=n
        buckets[digit] << n
      end
      ary = buckets.flatten
      p [i, ary] if $DEBUG
    end
    ary
  end
  def radix_sort!(base=10)
    replace radix_sort(base)
  end

Sources:

HERMAN, HOLLERITH. ART OF COMPILING STATISTICS. US395781A, 1889.

Cruz, Frank. “Columbia Difference Tabulator.” Columbia Difference Tabulator, http://www.columbia.edu/cu/computinghistory/packard.html.

Code: https://rosettacode.org/wiki/Sorting_algorithms/Radix_sort#Ruby